Bài toán “3 cái nhà 3 cái giếng” là một câu đố kinh điển sau đây:

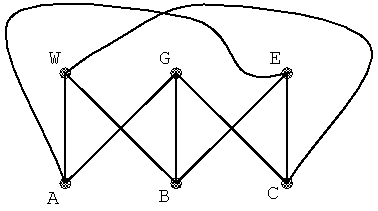
Có 3 cái nhà (hay nhà kho)  và 3 cái giếng  (hay nhà máy, trạm cung cấp gì đó). Người ta muốn xây 9 con đường nối từ các nhà đến các giếng, mỗi đường từ một nhà đến một giếng, sao cho không có hai con đường nào bị vắt lên nhau và không có con đường nào đi xuyên qua nhà khác hay giếng khác. Hỏi có thể làm được điều đó không?

Bài toán này có thể phát biểu dưới dạng lý thuyết đồ thị: Hình dung mỗi cái nhà và mỗi cái giếng là đỉnh của đồ thị, và mỗi con đường là cạnh của đồ thị, ta sẽ được đồ thi ký hiệu là (gồm có 2 bộ đỉnh, mỗi bộ 3 đỉnh, và cứ một đỉnh của bộ này và một đính của bộ kia thì có đúng một cạnh nối chúng, ngoài ra không có thêm cạnh nào khác). Câu hỏi là: đồ thì này có phải là đồ thị phẳng (planar graph) không?

Đồ thị phẳng là độ thị có thể vẽ trên mặt phẳng sao cho các cạnh không cắt nhau. Nói một cách chính xác hơn, một đồ thị gọi là phẳng nếu có thể nhúng nó qua một ánh xạ liên tục đơn ánh vào mặt phẳng.

Câu trả lời cho bài toán trên là:

Mệnh đề 1: không phải đồ thị phẳng

(Suy ra không thể xây được đường thỏa mãn các điều kiện của câu đố 3 cái nhà 3 cái giếng).

Để chứng minh điều này một cách chặt chẽ, ta cần dùng một kết quả sau:

Mệnh đề 2: Nếu một đồ thị là phẳng thì có thể nhúng nó (theo một đơn ánh liên tục) vào mặt phẳng sao cho các cạnh trở thành các đường gấp khúc.

(Phép nhúng như vậy gọi là phép nhúng đa giác – polygonal embedding). Nói cách khác, thay vì dùng các đường liên tục tùy ý, ta chỉ cần dùng đến các đường gãy khúc (gồm một số đoạn thẳng nối lại với nhau).

Sử dụng Mệnh đề 1, ta có thể xây dựng một cách chứng minh khá đơn giản cho định lý Jordan nổi tiếng sau:

Mệnh đề 3 (Định lý Jordan). Nếu là ảnh của một đơn ánh liên tục từ đường tròn vào mặt phẳng , thì không liên thông mà là hợp của hai miền liên thông, một “miền ngoài” không bị chặn và một “miền trong” bị chặn.

Đường cong trong định lý Jordan được gọi là đường cong Jordan: nó khép kín và không tự cắt.

Trong trường hợp mà đường cong Jordan có dạng đa giác (một đường gãy khúc), bất kể lồi hay lõm, thì định lý Jordan khá hiển nhiên, và có một thuật toán đơn giản để xác định một điểm cho trước là nằm  ở miền trong hay miền ngoài của đường Jordan: kẻ một tia từ điểm đó. Có thể chọn tia sao cho nó chỉ cắt đường Jordan một số hữu hạn điểm. Nếu số điểm cắt đó là số chẵn, thì điểm ban đầu nằm ở miền ngoài, còn nếu số điểm đó là số lẻ, thì điểm ban đầu nằm ở miền trong.

(Một đường cong Jordan: đâu là miền trong đâu là miền ngoài?)

Đối với các đường trơn (khả vi) theo khúc, định lý Jordan cũng khá dễ dàng chứng minh. Nhưng đối với các đường phức tạp hơn, không trơn theo khúc, thậm chí không khả vi tại điểm nào hết, có dạng fractal, xoắn lung tung nhì nhằng khắp khơi, v.v., thì việc xác định một điểm cho trước là điểm nằm ở miền trong hay miền ngoài nhiều khi không đơn giản tí nào, và tuy định lý Jordan về mặt trực giác thì có thể dễ cảm thấy là đúng, nhưng để chứng minh chặt chẽ thì khác phức tạp. Hơn nữa, mở rộng của định lý Jorrdan lên trường hợp 3 chiều không còn đúng, với phản ví dụ nổi tiêng mang tên ‘mặt cầu có sừng của Alexander‘ (Alexander’s horned sphere).

(Hình cầu có sừng của Alexander, ở Centre de Mathématiques et d’Informatique de Chateau-Gombert, Marseille)

Ở dưới đây chúng ta sẽ cố gắng đưa ra một chứng minh tương đối đơn giản cho định lý Jordan.

Schoenflies cải thiện kết quả của Jordan thành định lý sau:

Mệnh đề 4 (Định lý Jordan-Schoenlies) Nếu là một đường cong Jordan trên mặt phẳng , thì tồn tại một đồng phôi (homeomorphism) từ vào chính nó biến thành một đường tròn.

(Hệ quả: Miền trong của một đường cong Jordan thì đồng phôi với hình tròn, còn miền ngoài đồng phôi với hình cái vành).

Chứng minh Mệnh đề 2:

Giả sử ta nhúng được một đồ thị K vào mặt phẳng. Ta sẽ chứng minh rằng có thể thay đổi cách nhúng sao cho các cạnh của K đều trở thành những đường gấp khúc không cắt nhau.

Cố đinh ảnh các đỉnh của K trên mặt phẳng (không cần thay đổi chúng). Có thể giả sử các đỉnh cách nhau một khoảng lớn hơn 2 đơn vị. Với mỗi cạnh c đi từ đỉnh P đến đỉnh Q, gọi A là điểm “đi ra khỏi P” với khoảng cách 1, tức là khoảng cách từ P đến A bằng 1, và các điểm nằm trên c từ A đến Q đều cách P một khoảng lớn hơn 1. Gọi Z là điểm “đi vào tới Q” với khoảng cách 1, tức là khoảng cách từ Z đến Q bằng 1, và các điểm nằm trên c từ P đến Z đều cách Q một khoảng lớn hơn 1. (Theo tính chất liên tục, thì các điểm này tồn tại và duy nhất). Bây giờ ta chỉ việc thay khúc đường đi từ P đến A trên c bằng đoạn thẳng PA,  thay khúc đường đi từ Z đến Q trên c bằng đoạn thẳng ZQ, và thay khúc đường đi từ A đến Z bằng một đường gấp khúc không tự cắt xấp xỉ nó với độ lệch đủ nhỏ. Theo cách đó, mọị cạnh đều trở thành đường gấp khúc, và chúng vẫn không cắt nhau như trước. Ta đã chứng minh xong Mệnh đề 2.

Dùng Mệnh đề 2 thì việc chứng minh Mệnh đề 1 trở nên dễ dàng. Sau đó dùng mệnh đề 1 thì việc chứng minh Mệnh đề 3 bằng phản chứng trở nên dễ dàng. Cuối cùng, có thể chứng minh Mệnh đề 4 bằng cách xấp xỉ dần dần.

Chứng minh mệnh đề 1 (dựa vào Mệnh đề 2):

Giả sử là đồ thị phẳng. Theo Mệnh đề 1 có thể vẽ nó trên mặt phẳng, với các cạnh là các đường gấp khúc không cắt nhau. Gọi hai bộ đỉnh của đồ thị là A,B,C và X,Y,Z. Xét các “tứ giác”
AXBY (tạo bởi 4 cạnh gấp khúc) và BXCY. Chúng chia mặt phẳng thành 3 miền (hai miền “trong” và một miền “ngoài”), và ta có thể giả sử hai miền trong được bao bởi AXBY và BXCY. Đỉnh Z phải nằm ở một trong 3 miền đó. Nếu chẳng hạn Z nằm trong miền AXBY thì cạnh CZ sẽ phải cắt ít nhất một cạnh của tứ giác AXBY, vô lý. Các trường hợp khác cũng dẫn đến mâu thuẫn tương tự. Vậy không phải đồ thị phẳng

Chứng minh mệnh đề 2 (dựa vào Mệnh đề 1):

Ý tưởng (lấy từ sách của Katok) là chứng minh rằng nếu mà đường Jordan nào đó không chia mặt phẳng thành 2 phần thì xây dựng được một đồ thị phẳng đẳng cấu với , mâu thuẫn:

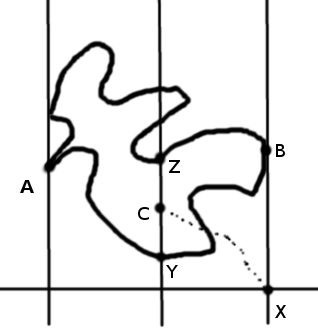Kẻ hai đường song song a và b tạo thành một dải kẹp đường cong Jordan vào bên trong, với một điểm A của trên a và một điểm B của trên b. Gọi x là một đường vuông góc với a và b và không cắt S. Gọi X là giao điểm của b và x. Kẻ một đường c song song với a và b và nằm giữa hai đường đó. Đường c cắt tại ít nhất 2 điểm, trong đó có điểm Y là điểm “cao nhất” mà nằm ở “nửa đường dưới”   của đi từ A đến B, còn Z là  điểm “thấp nhất” mà nằm ở “nửa đường trên”   của đi từ A đến B. Gọi C là một điểm nằm trên đoạn thẳng YZ. Khi đó, nếu như có một đường nối từ C đến X mà không cắt , thì những hình vừa xây dựng cho ta một đồ thị trong mặt phẳng, tức là là đồ thị phẳng, vô lý. Suy ra C và X phải nằm ở hai miền khác nhau của phần bù của trong mặt phẳng, tức là mặt phẳng trừ đi gồm có ít nhất 2 miền.

Tại sao lại chỉ có 2 mà không có nhiều hơn 2 miền? Để chứng minh điều này thì cần dùng đến bổ đề sau:

Mệnh đề 5 (Bổ đề). Nếu là một arc trên mặt phẳng (tức là ảnh của một đơn ánh liên tục ), thì hai điểm bất kỳ không nằm trên có thể nối được với nhau bởi một đường gấp khúc không cắt . Nói cách khác, phần bù của là một miền liên thông (theo đường gấp khúc).