(Bài viết cho Sputnik Newsletter số 04-2017)

Phạm Hi Đức

« Mundum regunt numeri » Euler đã từng quan niệm là thế giới bị các con số quản lý. Vậy sao ? Có thể nào quan điểm ngược lại, là toán bị dẫn dắt bởi vật lý thiên nhiên, gồm cả con người nữa, mới là đúng sự thật ?

Mặc dù Toán là môn trừu tượng và tìm kiếm cái luật vô hình đằng sau cái hữu hình, không ai phủ nhận được là rất nhiều khái niệm toán bắt nguồn từ đời sống hàng ngày. Chiêm tinh và kiến trúc đã khiến người Ai Cập và người Ba Bi Luân khai phá hình học. Và nghiên cứu máy móc bằng cơ học đã giúp cuộc Cách mạng Công nghệ của thế kỷ 17 cho chúng ta giải tích vi phân.

Trong thuyết lượng tử, những khái niệm toán học tiềm ẩn rất mạnh mẽ, mặc dù hàng ngày người ta không trải nghiệm được các hạt phân tử. Trong thế giới kỳ lạ của lượng tử, các vật thể thể hiện như là ở hai hay nhiều nơi cùng một lúc. Chỉ có sức mạnh của toán xác suất có thể diễn tả sự việc này. Không những toán trong tình huống này là một cách mô tả thiên nhiên một cách đầy đủ và thích ứng hơn tất cả các cách trước đây, mà ngược lại, vật lý lượng tử lại còn đem lại cho toán những thách thức rất bao quát và sâu xa để tiếp tục được khai triển. Các nhà nghiên cứu hy vọng khi ta hiểu và thấm nhuần cấu trúc thống nhất của thuyết lượng tử, nó sẽ giúp khai phá một ngành toán mới, « toán lượng tử ».

Trong vật lý cơ học cổ điển, người ta tính sự chuyển động của một thể vật đi từ điểm A đến một điểm B. Ví dụ, chuyển động sẽ đưa vật đó đi qua tất cả các điểm trên một quỹ đạo « tối ưu », một geô đê zích, theo một lộ trình ngắn nhất trong vũ trụ chứa đựng hai điểm đi và đến. Nhưng với khái niệm lượng tử thì khác. Thay vì chỉ một đường quỹ đạo, vật lý lượng tử xét toàn thể tập hợp của tất cả các lộ trình khả thi đi từ A, mặc dù nó dài hơn hay khúc khuỷu hay ngoặt ngoẹo hay vòng qua nửa vũ trụ trước khi bay về điểm B. (Đây là cái, mà nhà vật lý Richard Feynman ám chỉ qua cụm từ « tổng số các lịch sử »). Sau đó, theo cách tính toán của định luật lượng tử, mỗi lộ trình sẽ được phân cho một tỷ trọng diễn tả xác suất của là vật thể ta đang theo dõi, sẽ « chọn » bay theo lộ trình ấy. Như thế, phương án thường ngày ta gặp qua vật lý của Newton chỉ giản đơn là một phương án có xác suất cao nhất trong tất cả, chứ không phải phương án độc nhất. Cách nhìn vũ trụ như vậy, có thể rất phong phú về mặt triết lý, nhưng nó đem gì cụ thể cho toán học ? Ta hãy xem hai ví dụ sau đây.

Sự kiện I : Sự bất ngờ khi tính toán số đường cong độ N trong không gian Calabi-Yau

Lý thuyết dây là một thuyết hấp dẫn lượng tử, được xây dựng với mục đích thống nhất tất cả các hạt cơ bản cùng các lực cơ bản của tự nhiên, ngay cả lực hấp dẫn (theo Wiki tiếng Việt). Theo thuyết này, vạn vật trong nằm trong một vũ trụ không phải 3 chiều, mà 6 chiều hệ quả khi giải các phương trình hấp dẫn của Einstein. Các đáp án của các phương trình đó là những không gian gọi là Calabi-Yau, trong đó các chiều thặng dư ngoài 3 chiều quen thuộc được « cuộn » lại rồi « cất giấu » trong các hóc hiểm của không gian này.

Từ thế kỷ 19, người ta chứng minh rằng trong không gian Calabi-Yau đơn giản nhất, gọi là quintic, ta đếm được tổng số đường cong độ 1 (các đường thẳng) là 2875. Mãi đến năm 1980 người ta mới tính ra số đường cong độ 2 là 609 250. Năm 1990, một nhóm nhà vật lý chuyên về Thuyết dây cộng tác với các nhà toán hình học để tính số đường cong độ 3. Các chuyên gia hình học nghĩ ra một thuật toán và thiết kế một lập trình phức tạp để tính. Khi họ đưa con số cho các nhà vật lý, thì con số bị các nhà vật lý cho là sai. Khi kiểm tra lại, quả nhiên trong lập trình có nhầm lẫn. Nhưng sao các nhà vật lý lại « đón đầu » được các nhà hình học nhỉ ? Trong cộng đồng khoa toán, tất cả bị sốc khi khám phá ra là thách thức đếm trong không gian Calabi-Yau đã được các nhà vật lý giải đáp, không những đến độ 3, mà cả đến độ N bất kỳ, họ cũng tim ra cách tính.

Lý do là các nhà vật lý đã chuyển bài toán hình học thành một bài toán vật lý lượng tử. Do đó tất cả các độ N, (cũng như các sóng đứng với một số bất kỳ N điểm nút đều tuân theo một phương trình duy nhất) đã được phối hợp vào một phương trình tổng thể, mô tả làn sóng lan truyền qua không gian Calabi-Yau, và các nhà vật lý đã áp dụng phương thức giải theo cách « tổng số các lịch sử » nói trên. Mô hình một « dây », nhưng rung động theo các đường cong với tất cả các « độ » trong cùng khoảng khắc, đã là một ví dụ mà vật lý tạo ra một « ngành » toán cá biệt với tất cả định lý, chứng minh, đáp án, thuật toán của nó. Đây cũng là một trường hợp ứng dụng của « máy tính lượng tử » (quantum calculator)

Một không gian Calabi-Yau giản dị nhất : quintic (hình do wikipedia)

Sự kiện II : Độ cong của không gian và vật lý tương đối

Một ví dụ khác đã thể hiện giữa hình học và vật lý từ lâu đời hơn : đó là khi các phương trình của Einstein về sức hấp dẫn của các vật thể thiên văn tương đương với bài toán hình học mô tả chuyển động trên một mặt cong. Cái đối xứng giữa vật lý (sức hấp dẫn) và hình học (mặt cong không gian) khó chấp nhận cho những ai nghĩ là vũ trụ vật chất chỉ có một thực tế, và do đó chỉ có một cách độc nhất diễn tả qua toán.

Không kém khó hiểu là sự đối xứng giữa một hạt phân tử và hàm sóng của nó. Ngay từ đầu thế kỷ trước, các nhà vật lý học đã không ngớt tranh luận về cái nghĩa sâu xa của các phương trình chính họ đã khám phá ra : Niels Bohr, Wolfgang Pauli, Max Planck, Louis de Broglie … Con mèo (chết hay không chết) của Schrödinger, sự đo đạc chính xác không thể đạt, của cả vận tốc và vị trí cùng một lúc, của một vật theo định luật Heisenberg, tính cách của các phân tử, vừa là vật chất vừa là làn sóng di chuyển theo Loúi De Broglie … bấy nhiêu trường hợp mà 2 loại toán khác nhau tìm thấy sự đối xứng lẫn nhau nhờ xuyên qua cùng một thự tế vật lý.

Tóm lại, qua các lý thuyết lượng tử và tương đối, ta thấy toán và vật lý giúp nhau luân phiên đặt câu hỏi và đem đến cách giải.

* * *

Trong lãnh vực cổ điển hơn, ta cũng có tình trạng có hai hệ thống toán mô tả một thực tế hiện hữu duy nhất. Và ta cũng có một hình thức « tổng số các lịch sử » để tính ra con đường tối ưu. Cột trụ quan trọng của kết nối giữa toán và cơ học này là phép tính biến phân (Variational calculus).

Một cách hiểu toán biến phân là hoán chuyển các hàm số thực lên các « hàm của hàm số ». Toán biến phân là cách « tính đạo hàm » trên những hàm f (thí dụ giá du lịch) của các hàm u để kiếm ra những đáp án u* là hàm số tối ưu hoá hàm f.

Chẳng hạn giữa 2 điểm A và B ở toạ độ x₁ và x₂ ta kiếm tất cả các hàm số y(x), có đạo hàm bậc 2 liên tục. Ta kiếm hàm y* (lộ trình, kể cả cách điều hoà vận tốc y’*) tối thiểu hoá giá của cuộc du lịch gồm chi phí xăng, chọn đường dài ngắn, lái nhanh lái chậm v.v…

Nếu f là một hàm tối ưu hoá J thì ta có phương trình gọi là Euler-Lagrange :

Tại đây ta tìm thấy điểm liên kết tất cả những gì chúng ta bàn về « tổng số các lịch sử » trước : Phương trình Euler-Lagrange xem xét tất cả các « lịch sử » (khi x là thời điểm) hay nói cách khác, các « quỹ đạo » hay « lộ trình » f(x) (khi x là toạ độ), nhích từng ly từng tí dx trên mỗi lộ trình f(x) và xét soi xem cái giá phải trả L khi ta thay đổi một chút hàng ngang ∂f có được đền bù bằng một một lợi thế d(∂L/∂f’) về hàng dọc không ? Khi mà tại mỗi toạ độ x điều kiện này thoả, thì tập hợp tất cả các điểm x chính là lộ trình tối ưu.

Chỉ nhận xét sơ sơ qua, ta thấy vật lý dựa trên toán biến phân này, là một loại tư duy nhìn tổng thể tất cả cục diện (tất cả các biến khả thi) rồi mới tim ra tối ưu. Nó khác vật lý Newton, chỉ chú trọng vào từng vị trí một, từng véc tơ lực trong một thời điểm đứng, không liên quan gì đến lúc trước lúc sau của thời điểm đó.

Khi vào lãnh vực kinh tế tài chính, chúng ta cũng có ứng dụng của phương trình Euler-Lagrange. Nó diễn tả tình trạng tiêu thụ tối ưu, khi khoản vốn mà chúng ta để dành vào đầu tư (bằng cách nhịn tiêu xài hôm nay), sẽ đem đến ngày mai sự hài lòng trong đúng tỷ lệ mà ta chịu thiệt hôm nay.

Trong cuộc đời chúng ta, có dễ tính toán như trong toán học không ? Có thể dùng phép tính biến phân mà chi li từng giây phút, mình tự mặc cả với chính mình để phân chia sự thụ hưởng hôm nay với sự trả giá ngày mai cho đến cuối đời một cách tối ưu không ?

Việc đó đòi hỏi ta nhìn được suốt tương lai cuộc đời, như một tờ giấy báo trải dài dưới mắt, và có khả năng nhìn các việc quá khứ hiện tại vị lai cũng rõ ràng minh bạch như nhau. Nghĩa là ta làm chủ được thời gian …

Cách đây một số Sputnik, tôi biên một bài về cách Toán học trình bày thời gian (qua Emile Borel, Kolmogorov, và Nicole El Karoui). Bài đó nhấn mạnh về thời gian được xây dựng trong toán học như một chuỗi sụ kiện, mà phần nằm trong tương lai ta chỉ tiếp nhận được qua những xác suất của nó.

Đăng xong thì tôi đi xem phim viễn tưởng mới ra « Arrival » (« Cuộc đổ bộ bí ẩn »). Xem xong, xúc động mạnh vì chuyện tình cảm mẹ con trong đó lồng vào câu hỏi « nếu bạn biết sinh con, mà khi nó đến 17 tuổi, nó sẽ bỏ bạn mà đi một cách thảm thiết, thì bạn có sinh con không ? ». Câu chuyện nảy ra ngay từ cách dựng phim, ngay 5 phút đầu (tôi không spoil phim đâu) vì người ngoài hành tinh đem đến một cách vượt thời gian khá bất ngờ. Cách đặt vấn đề thời gian vừa đưa đến kết quả trái ngược với cách tôi trình bày trong bài báo Sputnik, mà cũng lại hoàn toàn … phù hợp với nó !

Nhắc lại, định nghĩa thời gian, theo ngành Giải tích ngẫu nhiên ứng dụng vào tài chính, đã được xây ra để diễn tả từng chuỗi các sự kiện khả dĩ đo được (theo nghĩa có thể phân định một « measure » trên tập hợp đó), để một mặt, ta ước lượng các xác suất của các sự kiện tương lai, mặt khác, khi thời điểm hiện tại biến tương lai thành quá khứ, dần dà khắc vào đồng vào đá, các sự kiện quá khứ để không ai thay đổi được. Như vậy thì rõ ràng, ai làm sao đi ngược dòng thời gian được ? Hệ quả tất yếu là không ai biết được tương lai.

Thế mà trong thiên nhiên quen thuộc của chúng ta có những sự việc cứ như là có những thể vật biết trước tương lai chúng sẽ ra sao : Nhìn nước mưa chảy trên một mặt dốc khúc khuỷu, để ý mà xem, nó sẽ luôn luôn chảy theo đường ngắn nhất đến cùng, mặc dù đôi khi lúc đầu dòng nước có vẻ đi theo một con đường khác hơn là theo độ dốc nhất. Làm sao mà nó biết, trước khi chảy đến chân mặt dốc ở thời điểm t = T, nó sẽ phải tối thiểu hóa

?

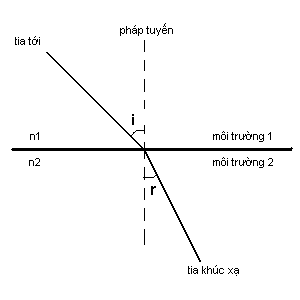
Phim đem cho tôi một cơn nóng lạnh vì nhận diện vấn đề này. Tôi đã phải bỏ 5€ mua cuốn sách căn bản của phim trên Amazon, và thích thú khi biết tác giả Ted Chiang đã có bằng Computer Science của Brown. Chuyện trong sách có nhiều trang để đi vào chi tiết, đặt vấn đề dơn giản hơn với sự kiện tia ánh sáng khúc xạ khi chiếu từ không khí vào trong nước. Làm sao nó biết phải theo định luật Snell

Và định luật này là một hệ quả tất yếu của việc con đường đi của tia sáng là con đường ngắn nhất, và nó cũng đi từ phép tính biến phân đã đề cập trên kia.

Con người và giọt nước khác và giống nhau thế nào ? Toán học có cho ta câu trả lời không ?

Theo tôi, và trên căn bản các điễu trình bày đoạn trên, toán học đơn độc thì không thể, nhưng toán với kinh tế và vật lý thì rất có thể có …

Phạm Hi Đức