Nguyễn Tiến Dũng

Bởi toán học là một thể thống nhất, nên không những chỉ “hình học chẳng qua là đại số được vẽ ra, đại số chẳng qua là hình học được viết ra” như theo lời của Sophie Germain, mà những thứ khác của toán học tưởng chừng “xa cách ngàn trùng” cũng nối kết khăng khít với nhau.

Một ví dụ rất hay về chuyện gắn kết này là bài toán tô màu (một vấn đề tổ hợp) và định lý điểm bất động (trong giải tích, tô-pô)

Trước hết, ta xét bài toán tô màu, là một bài toán tổ hợp sơ cấp sau đây:

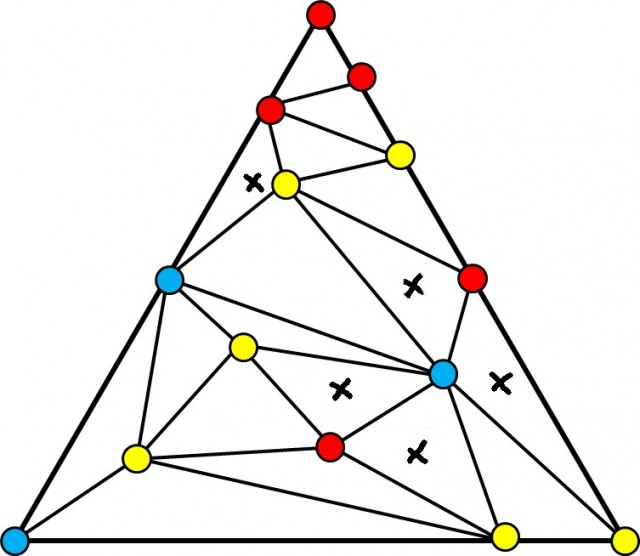Cho một tam giác ABC. Chia nó ra thành nhiều tam giác con một cách tùy ý. Tô màu các đỉnh của các tam giác con bằng 3 màu xanh, vàng, đỏ, sao cho: A tô màu xanh, B tô màu vàng, C tô màu đỏ, các đỉnh trên cạnh AB thì phải có màu là xanh hoặc vàng (giống như màu A hoặc B), các đỉnh trên cạnh BC thì phải có màu là vàng hoặc đỏ (giống màu của B hoặc C), và các đỉnh trên cạnh CA thì phải có màu là đỏ hoặc xanh (giống như màu của C hoặc A). Xem hình vẽ minh họa. Chứng minh rằng: Khi đó luôn tồn tại ít nhất 1 tam giác con có 3 đỉnh được tô bằng đủ 3 màu xanh, vàng, đỏ.

Bài toán trên được biết đến với tên gọi Bổ đề Sperner (Sperner’s lemma), do nhà toán học người Đức Emanuel Sperner (1905-1980) nghĩ ra trong một bài báo từ năm 1928.

Có cách chứng minh rất đơn giản sau đây cho bài toán trên:

Vẽ một đồ thị, trong đó có một đỉnh ứng với miền bên ngoài của tam giác ABC và mỗi đỉnh còn lại ứng với một tam giác con bên trong tam giác ABC. Mỗi cạnh của đồ thị ứng với hai miền (tam giác con hoặc miền bên ngoài) có chung nhau một cạnh có một đầu được tô màu xanh và một đầu được tô màu vàng. Số cạnh xuất phát từ đỉnh “ngoài” (tức là đỉnh ứng với miền nằm bên ngoài tam giác ABC) là một số lẻ (Vì sao vậy?). Suy ra có ít nhất một đỉnh “trong” có số cạnh cũng là số lẻ (vì tổng tất cả các số cạnh của tất cả các đỉnh là số chẵn, bằng 2 lần tổng số cạnh của đồ thị). Nhưng mỗi đỉnh trong ứng với một tam giác con, và số cạnh của nó chỉ có thể là 0, 1 hoặc 2 tùy theo các màu trên các đỉnh của tam giác con đó, và số đó là 1 khi và chỉ khi ba đỉnh có ba màu khác nhau xanh-vàng-đỏ. Vậy có ít nhất một tam giác con có ba đỉnh xanh-vàng-đỏ. Hơn thế nữa, số tam giác con như vậy phải là một số lẻ!

Bồ đề Sperner không những chỉ đúng trong trường hợp tam giác 2 chiều, mà còn đúng trong trường hợp n chiều trong đó n là một số tự nhiên bất kỳ. Khi n=1 thì nó phát biểu như sau:

Đánh dấu một số hữu hạn điểm trên một đoạn thẳng AB, chia nó thành một số đoạn thẳng con. Tô màu các điểm đó và A, B bằng hai màu xanh, đỏ sao cho a có màu xanh, B có màu đỏ. Khi đó có ít nhất một đoạn thẳng con có hai đầu có màu khác nhau xanh và đỏ. (Hơn thế nữa, số đoạn thẳng thẳng con như vậy là số lẻ).

Trường hợp 1 chiều phía trên của bổ đề Sperner khá là hiển nhiên và có thể chứng minh dễ dàng bằng quy nạp theo số điểm: cứ mỗi lần thêm 1 điểm thì số đoạn thẳng con có hai đầu có màu khác nhau hoặc là giữ nguyên hoặc là thêm 2, nên số lượng của chúng luôn là số lẻ. Trong lúc chứng minh bổ đề Sperner cho trường hợp 2 chiều, chúng ta đã dùng đến bổ đề 1 chiều này khi nói rằng số cạnh của đỉnh “ngoài” trong đồ thị mà ta xây dựng là một số lẻ.

Trong trường hợp 3 chiều, ta phải thay hình tam giác bằng một hình tứ diện ABCD, chia nó thành các hình tứ diện con, và tô các đỉnh bằng 4 màu (sao cho các đỉnh nằm trên mỗi mặt của ABCD phải có màu trùng với màu của một trong 3 đỉnh của mặt tam giác đó). Khẳng định vẫn là: số tứ diện con mà 4 đỉnh được tô bằng 4 màu khác nhau là số lẻ. Chứng minh vẫn hệt như cũ: xây dựng đồ thị với một đỉnh “ngoài” (ứng với miền nằm ngoài tứ diện) và các đỉnh “trong” (mỗi đỉnh ứng với một tứ diện con). Một cạnh nối hai đỉnh sẽ ứng với một mặt tam giác chung của hai miền mà có 3 đỉnh được tô bởi đủ 3 màu cho trước nào đó. Khi đó số cạnh của đỉnh “ngoài” là số lẻ (theo bổ đề Sperner hai chiều), suy ra có một số lẻ các đỉnh trong có số cạnh là số lẻ. Những đỉnh đó sẽ là những đỉnh có đúng 1 cạnh, và ứng với tứ diện con có 4 đỉnh được tô 4 màu khác nhau.

Cứ tiếp tục như vậy, bằng cách quy nạp theo số chiều, ta chứng minh được bổ đề Sperner trong trường hợp tổng quát với số chiều tùy ý.

Bây giờ, ta chuyển sang định lý Brouwer về điểm bất động, do nhà toán học Luitzen Brouwer (1881-1966) người Hà Lan chứng minh vào quãng năm 1910. (Jacques Hadamard cũng chứng minh kết quả này vào năm 1910 một cách độc lập, tuy nhiên không hiểu sao người ta gọi nó là định lý Brouwer mà không gọi là định lý Brouwer-Hadamard). Nó có thể phát biểu như sau:

Mọi ánh xạ liên tục từ một hình lồi đóng và bị chặn chiều bất kỳ vào chính nó có ít nhất một điểm bất động, tức là một điểm nằm trong sao cho .

Định lý Brouwer có rất nhiều ứng dụng trong toán học. Ví dụ như John Nash (nhà toán học đoạt giải Nobel về kinh tế) đã dùng định lý này để chứng minh sự tồn tại của các điểm ổn định Nash trong các trò chơi chiến lược.

Các cách chứng minh “thuần túy giải tích” của định lý Brouwer khá là rắm rối. Nhưng có một cách chứng minh rất trực giác và dễ hình dung và tương đối sơ cấp, dựa trên bổ đề Sperner! Chính vì vậy, người ta còn gọi bổ đề Sperner là “định lý Brouwer tổ hợp“. Cách chứng minh đó như sau:

Ta sẽ chứng minh trong trường hợp 2 chiều (trường hợp tổng quát hoàn toàn tương tự), và có thể giả sứ là tam giác . (Nếu nó không phải tam giác thì có thể kéo nó co dãn thành hình tam giác, nói theo ngôn ngữ chính xác thì là nó “đẳng phôi với tam giác”, nên kết quả không thay đổi).

Xét ánh xạ liên tục , và cố định một điểm nằm bên trong . Ta sẽ tô màu tất cả các điểm của , theo nguyên tắc sau: Nếu hướng của vector nằm kẹp giữa hai vector thì tô màu xanh, nếu nó nằm kẹp giữa thì tô màu vàng, nếu nó nằm kẹp giữa thì tô màu đỏ. Nếu chẳng hạn nó trùng hướng với thì chọn một trong hai màu vàng và đỏ. Ta có thể tô như vậy, sao cho có màu tương ứng là xanh, vàng, đỏ, không có điểm nào trên đoạn   có màu đỏ, không có điểm nào trên đoạn   có màu xanh, không có điểm nào trên đoạn   có màu vàng, như là trong bổ đề Sperner.

Chia thành các tam giác nhỏ dần và nhỏ dần, rồi áp dụng định lý Sperner, ta được một dãy các tam giác con của có đường kính nhỏ dần đến 0, sao cho các đỉnh của mỗi tam giác đều được tô bằng đủ 3 màu. Đặt tên lại các đỉnh nếu cần thiết, ta có thể giả sử các điểm đều có màu xanh, các điểm đều có màu vàng, các điểm đều có màu đỏ.

Sử dụng tính chất đóng và bị chặn (tức là tính chất compact) của , ta tìm được một dãy con của dãy điểm  hội tụ. Có thể giả sử luôn đó chính là dãy , và gọi giới hạn của nó là điểm . Vì kích thước của dãy tam giá tiến dần đến 0 nên ta có .

Sử dụng tính chất liên tục của ánh xạ $\latex f$, từ việc tất cả các vector  đều nằm kẹp giữa , ta suy ra nếu thì hướng của nó phải nằm kẹp giữa . Tương tự như vậy, hướng của nó phải nằm kẹp giữa , và cũng phải nằm kẹp giữa . Không thể như vậy, trừ khi , có nghĩa là điểm chính là một điểm cố định của ánh xạ .

Ta đã chứng minh xong định lý Brouwer.

Quay lại bổ đề Sperner. Có một trò chơi tam tác sau liên quan đến nó:

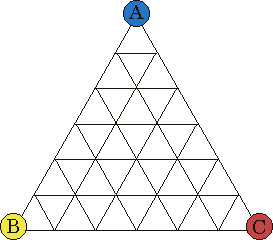Chia  tam giác ABC thành 36 tam giác con như trong hình vẽ. Ba đỉnh A, B, C của nó tô các màu anh, vàng, đỏ tương ứng. Hai người chơi lần lượt tô các đỉnh còn lại của các tam giác con, mỗi người chọn một đỉnh nào đó và tô khi đến lượt mình, sao cho các đỉnh trên cạnh AB phải là màu xanh hoặc vàng, trên cạnh BC phải là vàng hoặc đỏ, và trên cạnh CA phải là đỏ hoặc xanh. Số điểm của người thứ nhất là số tam giác con có các đỉnh được tô màu xnh-vàng-đỏ theo chiều ngược kim đồng hồ (cùng chiều với các màu tại ABC), còn số điểm của người thứ hai là số tam giác con có các đỉnh được tô màu xanh-vàng-đỏ theo chiều thuận kim đồng hồ. Ai được nhiều điểm hơn thì thắng. Theo bạn thì ai sẽ thắng, vì sao?

Chú ý rằng, theo bổ đề Sperner, tổng số điểm của hai người chơi là số lẻ, nên sẽ có người thắng và người thua chứ không hòa. Nhưng chi tiết hơn nữa, sự chênh lệch điểm giữa hai người có thể là bao nhiêu? Đây là bài tập dành cho bạn đọc :) Hay là đầu tiên cứ thử chơi vài ván xem?