Đây là các câu đố trong Sputnik Newsletter Số 2
Xin mời bạn đọc gửi lời giải về: newsletter@sputnikedu.vn
Thời hạn gửi lời giải: Đến hết tháng 02/2017. (Có thể chỉ giải một bài cũng được).
Chú ý ghi rõ họ tên, địa chỉ và số điện thoại liên lạc, lớp học (nếu có).
Những ai có lời giải hay sẽ được tuyên dương trên Newsletter và được tặng thưởng sách Sputnik.

Chú ý: Bạn đọc có thể gửi đến lời giải của những câu đố kỳ trước mà chưa công bố lời giải.

Câu đố 2-1 (Điểm nguyên). Cho một hình ngũ giác lồi bất kỳ trên mặt phẳng với một hệ tọa độ cho trước, với các đỉnh đều là điểm nguyên. (Điểm nguyên là điểm có các tọa độ đều là số nguyên). Các đường chéo của hình ngũ giác này cắt nhau tạo thành một hình ngũ giác nhỏ bên trong. Chứng minh rằng hình ngũ giác chứa ít nhất một điểm nguyên ở bên trong hoặc trên biên của nó.

Câu đố 2-2 (Che vết bẩn). Trên một mặt bàn phẳng có một vết ố có đường kính 5 cm. (Đường kính của một hình là khoảng cách lớn nhất giữa hai điểm của hình đó). Chứng minh rằng có thể phủ kín vết ố đó bằng một tấm lót tròn có bán kính 3 cm.

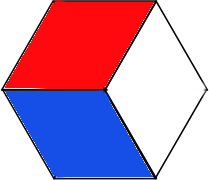
Câu đố 2-3 (Bài toán xếp kẹo). Có một hộp kẹo hình lục giác đều mỗi cạnh dài 3 cm, để xếp các viên kẹo hình thoi mỗi cạnh dài 1cm và góc nhọn bằng . (Hình thoi này là hợp của hai hình tam giác đều). Dễ thấy có thể xếp vừa khít 27 viên kẹo vào hộp. Bây giờ giả sử các viên kẹo có một trong 3 màu: trắng, xanh, đỏ. Đặt hộp sao cho một cạnh của nó nằm ngang phía dưới. Các viên kẹo màu trắng phải được xếp sao cho đường chéo dài của nó có hướng thẳng đứng từ dưới lên trên, các viên kẹo xanh phải xếp sao cho đường chéo dài của nó có hướng chếch từ trên xuống dưới khi nhìn từ trái sang phải, còn các viên kẹo đỏ phải xếp sao cho đường chéo dài của nó có hướng chếch từ dưới lên trên khi nhìn từ trái sang phải (xem hình vẽ). Dễ thấy có thể xếp như vậy với đúng 9 viên kẹo trắng, 9 viên kẹo xanh và 9 viên kẹo đỏ.

a) Nếu số kẹo trắng khác 9 (và tổng số kẹo vẫn là 27) thì có thể xếp kín hộp sao cho điều kiện phía trên được thỏa mãn không? (Đưa ra ví dụ hoặc giải thích thỏa đáng).

b) Có tổng cộng bao nhiêu cách xếp kẹo khác nhau (với các viên kẹo trắng, xanh, đỏ) thỏa mãn điều kiện trên?