Đây là một vấn đề thuật toán hết sức thú vị, và trường hợp riêng của nó đã được đem làm câu đố cho Spunik Newsletter Số 2. Chúng tôi xin trình bày lại nó thành riêng một bài dưới đây:

a) Bạn có thể đã nghe nói về bài toán Tháp Hà Nội: Có 3 cái cột, và có 8 miếng gỗ tròn có đục lỗ ở giữa được xếp vào cột thứ nhất tạo thành hình một cái tháp, sao cho miếng ở trên nhỏ hơn miếng ở dưới (tựa như các tầng tháp ở các ngôi chùa càng lên cao càng nhỏ dần).  Bây giờ cần dịch chuyển các miếng tròn giữa các cột với nhau, với nguyên tắc miếng to hơn thì không được xếp lên trên miếng thấp hơn, sao cho cuối cùng di chuyển được toàn bộ cái tháp từ cột thứ nhất sang cột thứ ba. Hỏi phải làm thế nào, và di chuyển mất (ít nhất) bao nhiêu nước? (Mỗi nước là di chuyển một tầng tháp từ cột này sang cột khác). Nếu thay số 8 bằng một số n bất kỳ thì sao?}

b) Bây giờ chúng ta thay các các cột bằng các cái ghế, và các tầng tháp hình tròn bằng các miếng phó mát tròn kích cỡ tăng dần từ nhỏ đến to, thì bài toán vẫn như vậy. Nhưng bây giờ, thay vì có 3 cái ghế, ta có những 4 cái ghế, và được di chuyển các miếng phó mát giữa các ghế đó (với điều kiện như cũ: phó mát ở mỗi ghế phái xếp thành chồng, và không được để miếng to lên trên miếng nhỏ), thì cần ít nhất là bao nhiêu bước di chuyển để chuyển toàn bộ chồng phó mát gồm 8 miếng từ ghế thứ nhất sang ghế thứ tư?

c) Nếu thay vì 8 miếng phó mát và 4 ghế, ta có một chồng 11 miếng phó mát và 4 ghế thì sao? Cần bao nhiêu bước?

Câu đố này là cải biên từ câu đố đầu tiên trong quyển sách rất thú vị nhan đề  Những câu đố tư duy và lô-gic xứ Canterbury (Tủ sách Sputnik số 026) của tác giả Dudeney. Có thể mở rộng nó lên trường hợp n miếng phó mát và k ghế, tìm số bước di chuyển ít nhất.

a) Trong trường hợp chỉ có 3 ghế (trò chơi Tháp Hà Nội), thuật toán khá là hiển nhiên: Cần chuyển chồng phó mát sang ghế thứ 2 rồi mới nhấc được miếng phó mát to nhất dưới cùng sang ghế thứ 3, rồi mới chuyển được chồng miếng phó mát sang ghế thứ 3. Giả sử là ta không làm các động tác nào thừa (như kiểu làm một số bước dịch chuyển, mà sau đó trạng thái các chồng phó mát vẫn hệt như cũ) thì chỉ có mỗi cách làm như trên thôi, và ta có công thưc quy nạp:

(bởi vì để chuyển miếng phó mát từ cột đầu tiên sang cột thứ hai thì mất   bước, v.v.).

Từ công thức quy nạp này ta suy ra .

b) Trường hợp có miếng phó mát (ở đây )  và 4 ghế hoặc nhiều hơn, thuật toán tối ưu cũng phải là thuật toán “không có những bước thừa”. Lý luận để loại đi những hành động thừa, ta có thể thấy rằng thuật toán tối ưu phải gồm những công đoạn như sau:

– Công đoạn 1: Chuyển miếng phó mát trên cùng () từ ghế thứ nhất sang ghế thứ hai, mất bước.

– Công đoạn 2: Chuyển miếng phó mát tiếp theo từ ghế thứ nhất sang ghế thứ 3, mất bước. (Chú ý rằng trong công đoạn 2 này thì không dùng được ghế thứ hai vì có những miến phó mát nhỏ hơn đặt ở đó, nên bài toán trở thành di chuyển với 3 ghế)

– Công đoạn 3: Chuyển miến phó mát to nhất sang ghế thứ tư, mất 1 bước.

– Công đoạn 4: Chuyển chồng phó mát từ ghế thứ ba sang ghế thứ tư, mất bước,

– Cộng đoạn 5: Chuyển nốt chồng phó mát từ ghế thứ hai sang ghế thứ tư, mất bước

(Ba công đoạn 2-3-4 có thể gộp thành một).

Tổng cộng, ta mất bước di chuyển,
và ta được công thức quy nạp:

Chú ý rằng, với mỗi , ta phải chọn tương ứng sao cho tổng là nhỏ nhất.

Vì nói chung khi có nhiều ghế thì sẽ mất ít bước di chuyển hơn là khi chỉ có ít ghế, tức là ta luôn có với mọi , nên dễ thấy là tối ưu phải thỏa mãn điều kiện . Trong trường hợp thì chỉ có thể nhận một trong 4 khả năng là 4,5,6 hoặc 7. Để so sánh các khả năng đó, ta phải lần lại theo quy nạp, tính ra ,  , . Từ đây ta suy ra đối với thì tối ưu là 5, và ta có

Đáp số: Trong trường hợp 8 miếng phó mát và 4 ghế  thì thuật toán tối ưu dùng 33 bước.

Câu c) với11 miếng phó mát phân tích tương tự, bạn đọc thử tự tính toán.

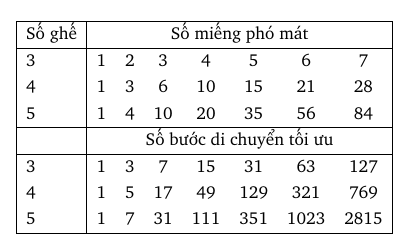
Trong sách  Những câu đố tư duy và lô-gic xứ Canterbury, Dudeney đưa ra một bảng để tính số bước tối ưu trong các trường hợp mà số ghế là và số phó mát là những số thích hợp nào đó.

Lập  một bảng như sau: Hàng đầu tiên bao gồm các số tự nhiên liên tiếp. Hàng thứ hai nhận được bằng cách cộng tổng các số tính từ số đầu tiên của  hàng thứ nhất, ví dụ là số thứ ba của hàng thứ hai  (các số này có dạng , gọi là các số tam giác). Hàng thứ ba nhận được bằng cách cộng tổng các số tính từ số đầu tiên của hàng thứ hai, ví dụ $1+3+6 = 10$ là số thứ ba của hàng thứ ba.  Hàng thứ tư là dãy các số có dạng .

Hàng tiếp theo nhận được bằng cách nhân đôi số phía trước rồi cộng thêm với số phía trên, ví dụ là số thứ tư của hàng này. Hàng cuối cùng cũng nhận được theo cùng công thức quy nạp
như hàng thứ năm.

Bảng này cho ta kết quả trực tiếp cho trường hợp 3 ghế và số miếng phó mát bất kỳ,  trường hợp 4 ghế với số miếng phó mát dạng tam giác (tức là các số ), và trường hợp 5 ghế với số miếng phó mát dạng hình chóp. Trong những trường hợp này, có thể chỉ ra phương pháp tối ưu như sau:

Trong trường hợp nhiều hơn 3 ghế: thuật toán dựa trên quy nạp và  phương pháp tách chồng theo như các công đoạn ghi phía trên. Chẳng hạn nếu có 4 ghế và 10 miếng phó mát thì ta làm như sau: Ta di chuyển 6 miếng phó mát ghế thứ nhất sang ghế thứ hai mất bước, rồi di chuyển 4 miếng phó mát còn lại  từ ghế thứ nhất sang ghế thứ tư mất bước, rồi di chuyển 6 miếng phó mát từ ghế thứ hai sang ghế thứ tư, mất thêm bước nữa, tổng cộng là bước.

Theo bảng của Dudeney, chúng ta nhận thấy, chẳng hạn khi có 4 ghế và số phó mát là một số dạng thì phải chọn số  tương ứng bằng . Nhưng vì sao số này lại là số tối ưu thì Dudeney không giải thích. Bạn có thể giải thích vì sao được không?